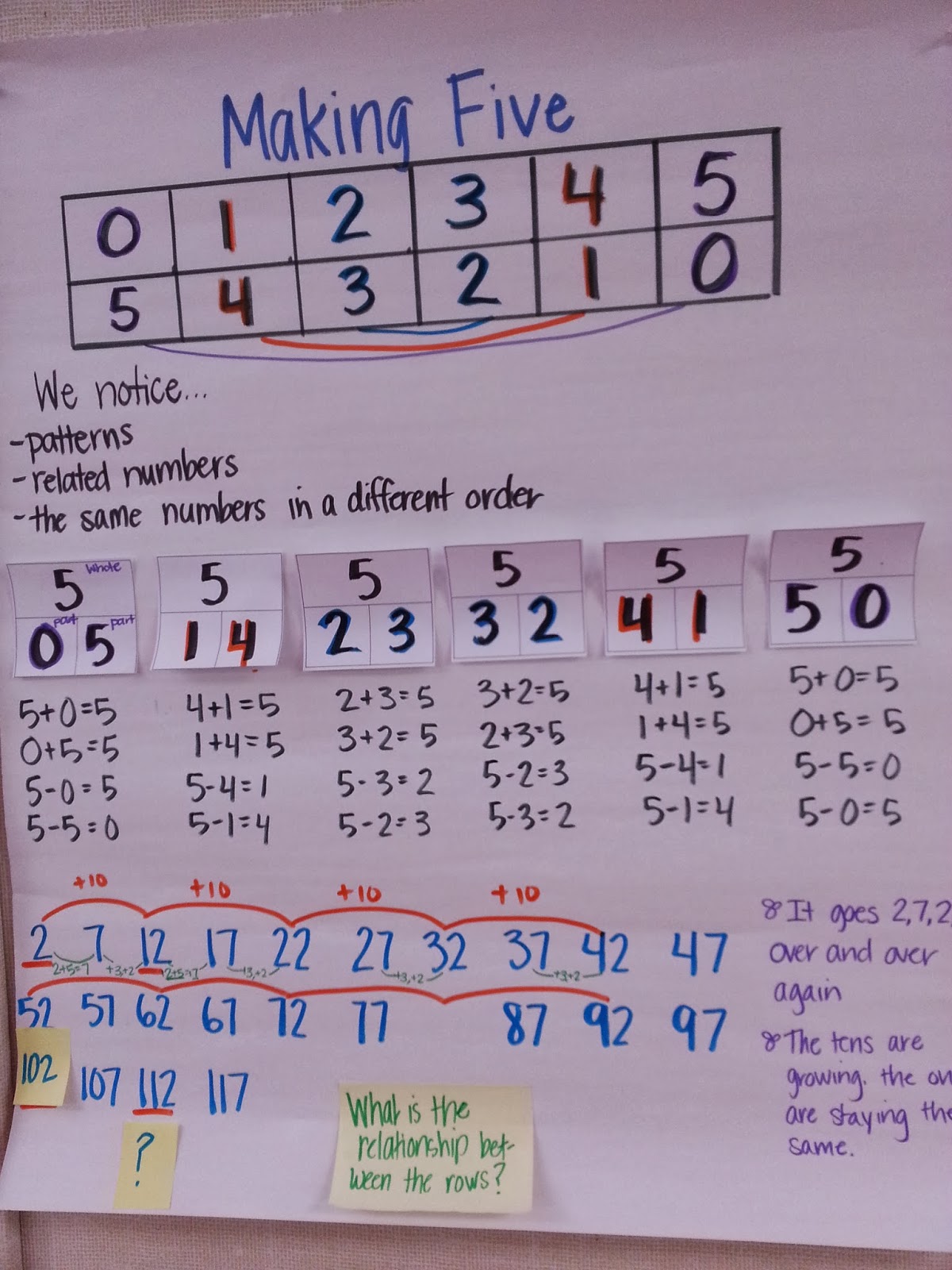
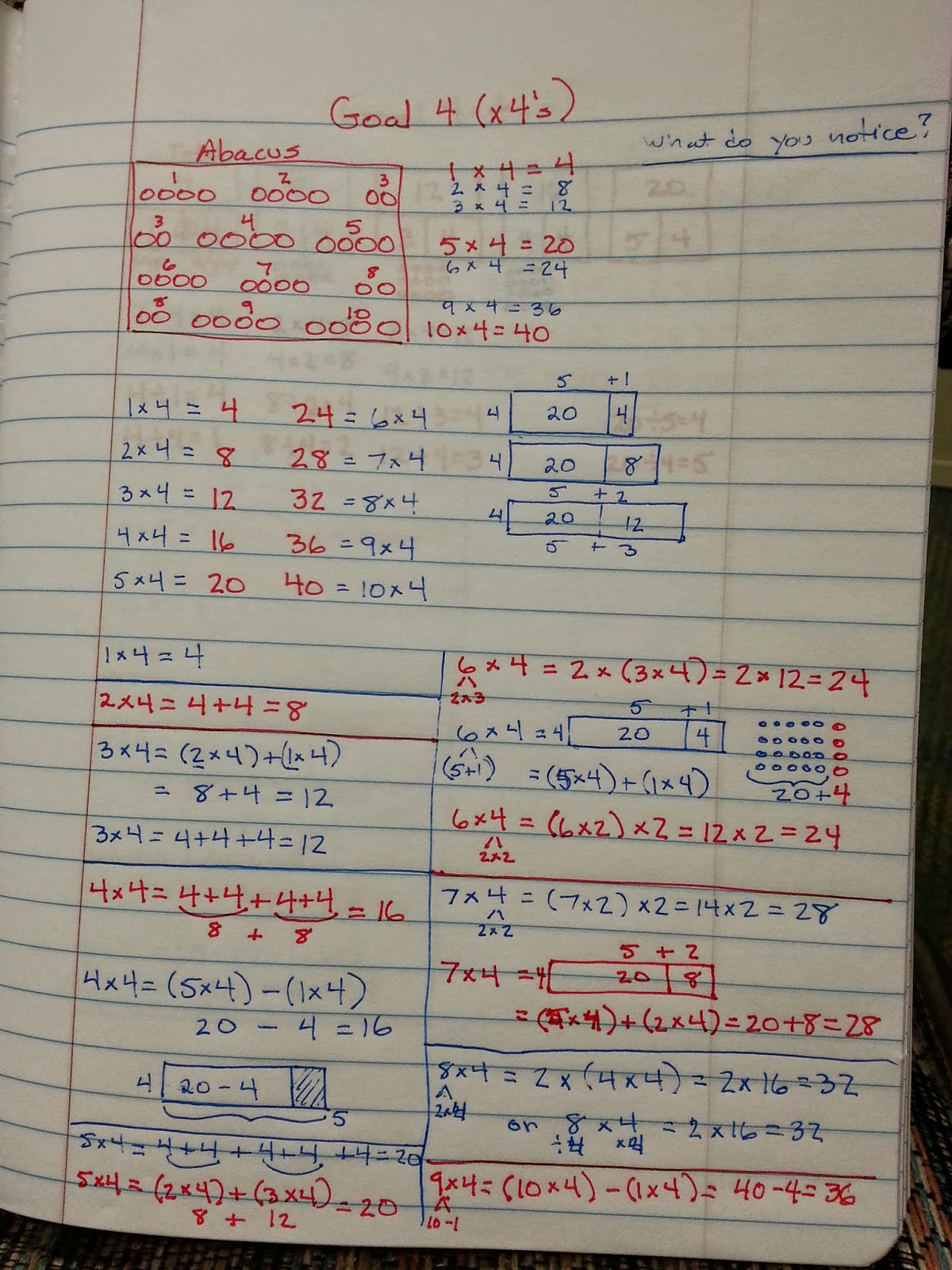The key idea behind all of these activities is the connection between concrete objects and/or representations and counting. I hope you and any of your students that need support with counting will enjoy these interactive activities!
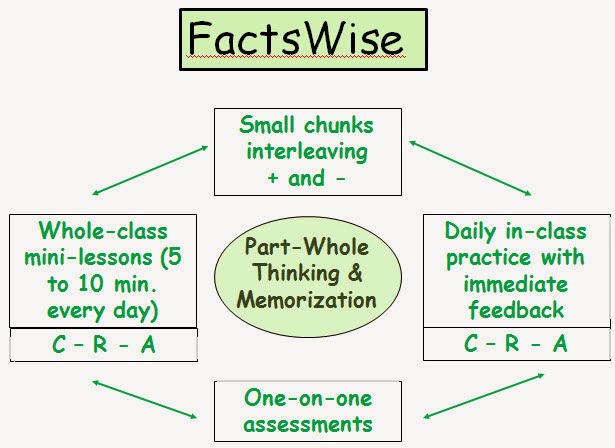
Building number sense and basic facts fluency for addition, subtraction, multiplication and division. Daily mini-lessons, games, and strategies based on properties of operations produce remarkable results.
Tuesday, October 28, 2014
Counting Comes First!
Before students can develop part-whole thinking, they need to understand how our numbers work and become confident counters. Here are a series of activities that can help students develop their understanding and fluency with counting.

Friday, June 20, 2014
A FactsWise Friendly Online Multiplication Game
I haven't found many online games that align well with the principles we talk about in FactsWise. Here's one game, though, that might prove helpful when students are ready for abstract work on a particular goal: Quick Flash II.
Even though this game starts out with little graphic interest, students get to earn their way to more interesting backgrounds.
Some of the features of this game that make it a good learning experience (in contrast to a good review experience), are:
1) Students can concentrate on the facts from one goal;
2) Students get immediate feedback;
3) Students get multiple opportunities to rehearse the same facts;
4) Students, teachers, and parents can see which facts are less fluent. Although there isn't a built-in feature for this, if you have your student press the "print screen" key on their computer as they finish the last problem on the third round, the game will pause (at least on my computer) and you can record the problems that aren't all green, or take a screen shot and then paste it into a word document.
At Your Request - Multiplication/Division Flower Representations
I hope you're all enjoying the start of summer! I just finished working with a great group of teachers who tried out a new idea -- flower representations for Goals 3, 4, and 5.
Goal 3 (x 2s)
Goal 4 (x 4s)
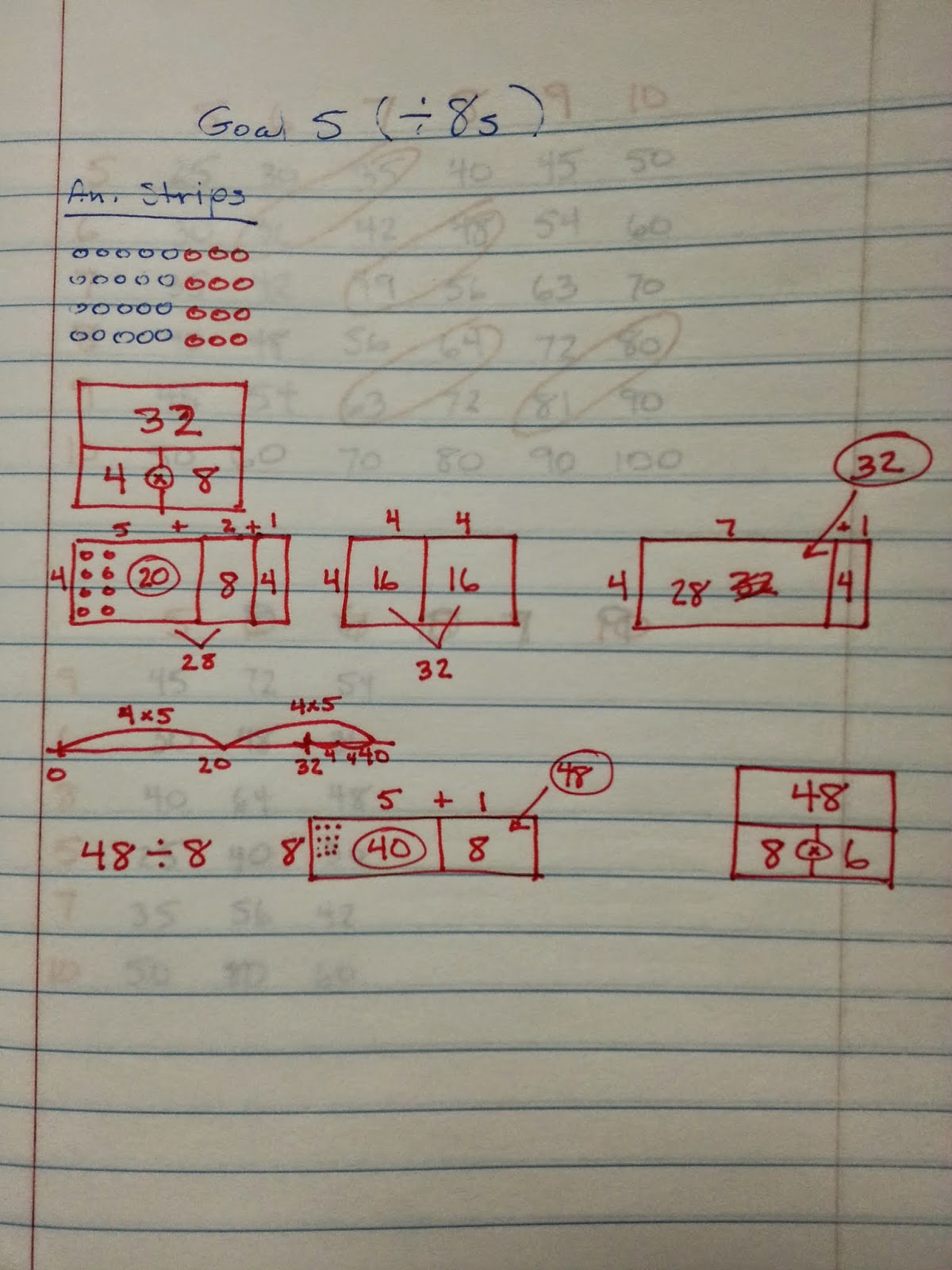
Goal 5 (x 8s)
Students can share copies of these flowers, and can work together to answer questions such as: "What do you notice?" and "How can the patterns you're noticing help you remember your facts for this goal?".
After students have found many of the patterns, you may want to organize the numeric patterns in two rows so that students can see the distributive property in action. For instance, with Goal 5, it could look like this:
Students will be able to notice the patterns, that 48 is 40 more than 8, 56 is 40 more than 16, and so on. With your help, they can figure out that this pattern happens because of the distributive property, and because 5 x 8 makes 40. Since 40 is a "friendly 10", the ones place repeats. For instance:
8 x 1 = 8
+ 8 x 5 = 40
8 x 6 = 48 or, more traditionally 8 x 6 = 8 x (1 + 5) = (8 x 1) + (8 x 5) = 8 + 40 = 48
8 x 2 = 16
+ 8 x 5 = 40
8 x 7 = 56 or, more traditionally 8 x 7 = 8 x (2 + 5) = (8 x 2) + (8 x 5) = 16 + 40 = 56
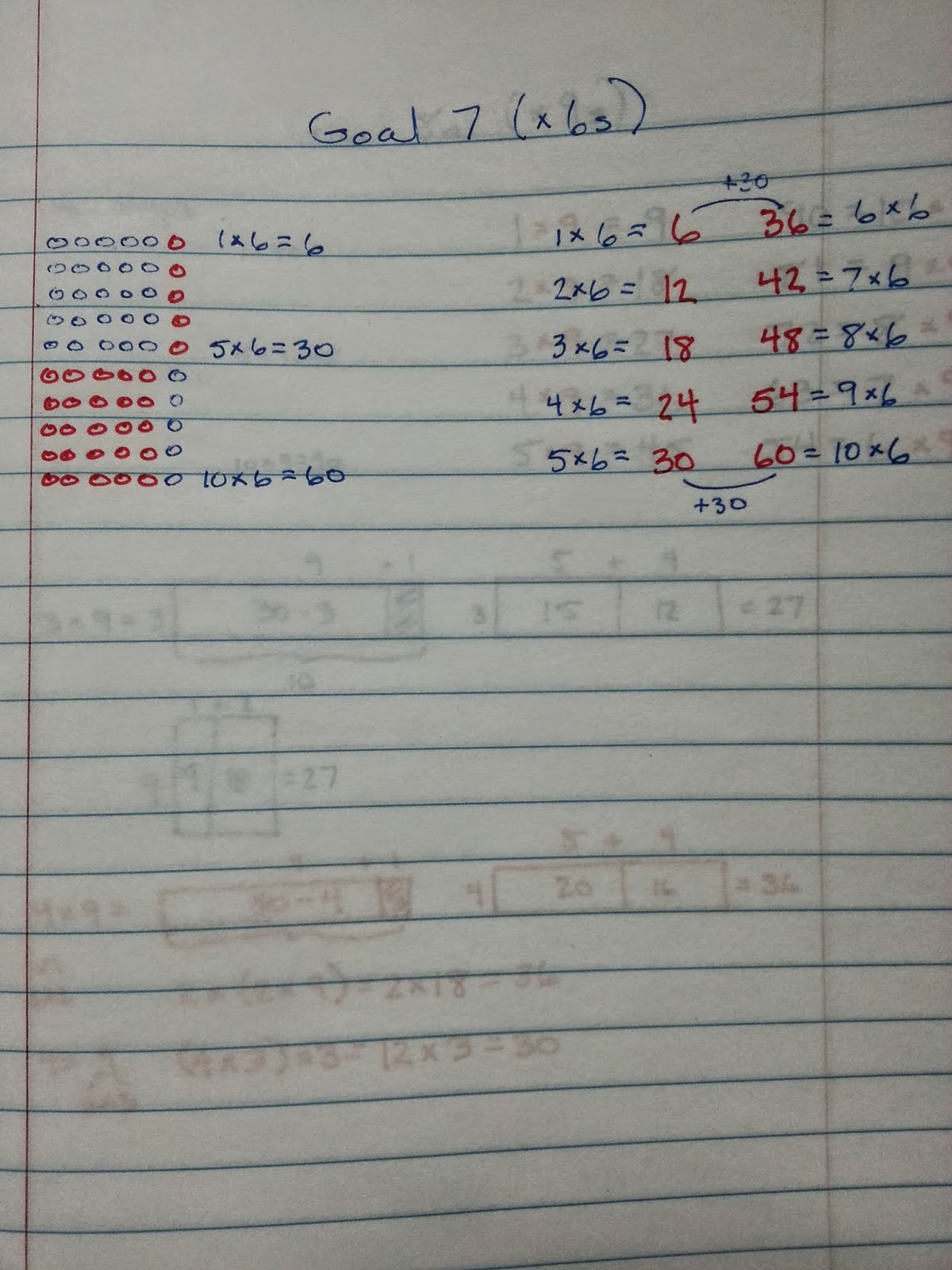
The distributive property helps explain similar patterns for Goal 3, Goal 4, and Goal 7 as well.
2 x 4 = 8
+ 2 x 5 = 10
2 x 9 = 18 or, more traditionally 2 x 9 = 2 x (4 + 5) = (2 x 4) + (2 x 5) = 8 + 10 = 18
This "friendly ten" pattern shows up in all of the even factor goals (e.g., x2, x4, x6, and x8).
And, since Goal 7 is part of the 3s, 6s, 9s sequence, I decided to change the image from flowers to apples. It's also on the "flowers" file linked at the top of this post.
If you decide to use these with students, it would be great if you could share what you and your students learned. I hope you all enjoy looking for patterns and making connections to algebraic thinking!
Tuesday, May 20, 2014
Multiplication/Division Chart Planning - Samples
I've been thinking about charting each of the different multiplication/division goals -- how to build in a concrete experience, at least one or two representations, a connection to properties and/or patterns, and a connection between multiplication and division. Here are my initial ideas -- I'd love to see what you wind up charting in your classrooms!
At Your Request: C-R-A Overview
In order to clarify what may be considered concrete, representational, and abstract activities, I've made a chart that I hope will help. Let me know what you think!
Thursday, March 13, 2014
Hands Cards for Games Focusing on 5s and 10s
I enjoyed visiting with a group of teachers this afternoon, where I shared a set of hand cards that can be used to play Addition War with any of the numbers facing up as the addend. For instance:
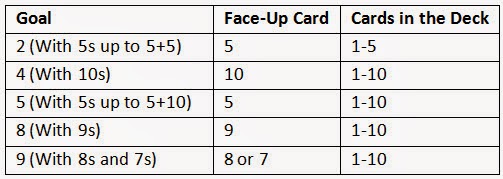
Sample Goal 5 Game Set-Up
Val's Card Calvyn's Card
In this round, Val turns up the top card of her stack and says "5 + 6 makes 11". Then Calvyn turns up his top card and says "5 + 8 makes 13". Since Calvyn has the larger sum, he gets both the 6 and 8 cards and puts them at the bottom of his stack. The 5 stays face up, so that every time they take turns they are practicing adding 5 to another addend.
You can download the Hand Game Cards here. If you think you'll have more than two students playing together, you may want to print and cut out more than one set of the cards for each deck.
As always, I encourage you to have students share, in writing or through a whole-class discussion, strategies they found helpful and facts they were learning as a result of playing the game.
Sample Goal 5 Game Set-Up
Face-Up Card
In this round, Val turns up the top card of her stack and says "5 + 6 makes 11". Then Calvyn turns up his top card and says "5 + 8 makes 13". Since Calvyn has the larger sum, he gets both the 6 and 8 cards and puts them at the bottom of his stack. The 5 stays face up, so that every time they take turns they are practicing adding 5 to another addend.
You can download the Hand Game Cards here. If you think you'll have more than two students playing together, you may want to print and cut out more than one set of the cards for each deck.
As always, I encourage you to have students share, in writing or through a whole-class discussion, strategies they found helpful and facts they were learning as a result of playing the game.
Tuesday, February 18, 2014
Sharing Recent Add/Subtract Powerpoint
I've done some major updates on the FactsWise Addition/Subtraction powerpoint over the past couple of months, and have been exploring different options for sharing it. It looks like my Dropbox account should do the trick. If you want to view or download the file, here's the link.
And here are a couple of slides that folks specifically asked for:
Sunday, January 5, 2014
At Your Request - Goal 2 Animal Strips Handout (Snails)
When introducing Goal 2 (x 5s), it can be helpful to have students focus first on the even factors of 5. Students can use an animal strips handout that helps them see the multiples of 10 patterns.
Once students are fluent with products of the even factors of 5, then they can work on the odd factors of 5. Students will be able to use the distributive property frequently with this approach. For instance:
7 x 5 = (6 x 5) + (1 x 5) = 30 + 5 = 35
You can also use the snails handout as students begin working on Goal 2 division. "How many groups of 5 snails are in 30 snails?"
At Your Request - New Multiplication/Division Flashcards
After hearing from teachers how well the factor-factor-product grids have been helping students make connections between multiplication and division, I spent some of the winter holiday making flashcards with these grids.
You have a couple of different options to choose from if you want to use these with your students. If you want to save paper, option 1 below is the way to go. If you want to have each goal start on a new page, and have a set that includes both multiplication facts (e.g., 2x3 and 3x2), then you'll want to use option 2. And if you have students who are ready for the Top 21 facts, use option 3.
- FactsWise Multiplication/Division Flashcards - Factor-Factor-Product Grids - Paper Saver
- FactsWise Multiplication/Division Flashcards - Factor-Factor-Product Grids - Complete
- FactsWise MD Top 21 Flashcards - Factor-Factor-Product Grids
It's also important to teach students how to use flashcards effectively:
- Focus on just one goal at a time to start. (Later on you can put two or more goals together when reviewing.)
- Look at the front of each flashcard. If you think you know the answer, check the back of the flashcard. If correct, then decide whether you knew it "fluently" -- within 2 seconds, without having to count to figure it out. If you knew the fact fluently, place the flashcard in a pile with other "fluent" facts. If you had to count, take more than 2 seconds, or didn't know the correct answer, place the flashcard in a "Still Working On It" pile.
- Once you've gone through all of the facts for the goal you're working on, now concentrate on the "Still Working On It" flashcards. Practice those facts several times. When you notice that you are developing fluency with a fact, you can move it to your "Fluent" pile.
- When you have moved all of the facts to your "Fluent" pile, then go back through the entire set of flashcards and decide if they are really fluent or whether you need to move some back to the "Still Working On It" pile again.
- Be sure and work on these same facts several days in a row, until you can put every fact in the "Fluent" pile in your first run through the cards. Make sure you shuffle the cards frequently so that you are truly learning the facts, and not just the order you're used to.
Subscribe to:
Posts (Atom)
Timed Tests -- NOT the Way to Build Facts Fluency and NOT the Way to Assess Facts Fluency
If you'd like to learn more about FactsWise, you can freely preview a number of the FactsWise mini-lessons and game...
-
If you'd like to learn more about FactsWise, you can freely preview a number of the FactsWise mini-lessons and game...
-
When we look at all the different topics that need to be covered every day, it's easy to see how basic facts can slip through the cracks...
-
After hearing from teachers how well the factor-factor-product grids have been helping students make connections between multiplication and ...





.jpg)
.jpg)
.jpg)